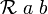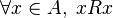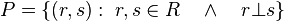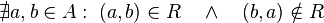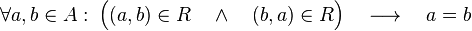CLASIFICACION POR TIPOS DE RELACIONES

clasificación por tipos de relaciones.

Relación BINARIA

En matemáticas, una relación binaria es una relación matemática R entre los elementos de dos conjuntos A y B. Una relación de este tipo se puede representar mediante pares ordenados, $(a,b)\in A \times B$

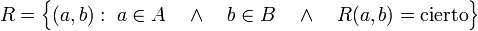
$R = \Big\{ (a,b): \; a \in A \quad \land \quad b \in B \quad \land \quad R(a,b) = \mbox{cierto} \Big\}$

Las proposiciones siguientes son correctas para representar una relación binaria $R\,$ :

$a \mathcal{R} b \qquad \mbox{o} \qquad R(a,b) \qquad \mbox{o bien} \qquad (a,b) \in R$

También puede expresarse:

$\mathcal{R} \; a \; b$

Propiedades de las relaciones binarias homogénea:

Una relación binaria puede tener ciertas propiedades, según los pares ordenados que formen parte de dicha relación o no formen parte de ella, veamos algunas:

Propiedad reflexiva:

Una relación binaria R sobre un conjunto A, es reflexiva o refleja si todo elemento de A está relacionado consigo mismo mediante R.

Es decir,

$\forall x\in A, \; xRx$

En tal caso, decimos que R cumple con la propiedad de reflexividad.

La aplicación de cualquier relación R sobre un conjunto A, se representa con el par ordenado (A, R).

Cuando una relación es lo opuesto a una reflexiva, es decir, cuando ningún elemento de A está relacionado consigo mismo mediante R, entonces decimos que es irreflexiva, antirreflexiva o antirrefleja, lo que denotamos formalmente por:

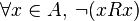
$\forall x\in A, \; \neg(xRx)$

Propiedad irreflexiva:

Una relación binaria: R, entre los elementos de un conjunto: A, es una relación irreflexiva, también llamada: antirreflexiva o antirrefleja, si ningún elemento del conjunto esta relacionado consigo mismo:

$\forall a \in A : \; (a,a) \notin R$

Para todo a que pertenezca a A, (a,a) no pertenece R.

Que también puede expresarse

$\nexists a \in A : \; (a,a) \in R$

No existe ningún elemento a en el conjunto A que cumpla que: (a,a) pertenezca a R.

Tomando las rectas en el plano:

$r, s, t, u, \dots$

Que forman el conjunto de las rectas del plano R:

$R = \{ r, s, t, u, \dots \}$

y la relación de perpendicularidad entre rectas P:

$P = \{ (r,s): \; r, s \in R \quad \land \quad r \bot s \}$

La relación binaria, formada por los pares de restas que son perpendiculares, que podemos representar:

$r \bot s \qquad \acute{o} \qquad \bot (r,s) \qquad \acute{o} \; bien \qquad (r,s) \in \bot$

Vemos que la relación de perpendicularidad entre rectas es irreflexiva, dado que para toda recta r del plano, r no es perpendicular a si misma.

$\forall r \in R : \; r \not \! \! \bot r$

Que también puede expresarse:

$\forall r \in R : \; \neg (r \bot r)$

Propiedad simétrica

Artículo principal: Relación simétrica.

Una relación binaria tiene la propiedad simétrica, si se cumple que un par ordenado (a,b) pertenece a la relación entonces el par (b,a) también pertenece a esa relación:

$\forall a, b \in A : \; (a,b) \in R \quad \longrightarrow \quad (b,a) \in R$

Para todo par ordenado (a,b) que pertenezca a R, implica que el par (b,a) también pertenece a R, téngase en cuenta que si el par (a,b) no pertenece a la relación el par (b,a) tampoco tiene que pertenecer a esa relación:

$\nexists a, b \in A : \; (a,b) \in R \quad \land \quad (b,a) \notin R$

No existe ningún par ordenado (a,b) que pertenezca a R y que el par (b,a) no pertenezca a R.plo

Propiedad antisimétrica

Artículo principal: Relación antisimétrica.

Una relación binaria se dice que tiene la propiedad antisimétrica si los pares ordenado (a,b) y (b,a) pertenecen a la relación entonces a = b:

$\forall a,b \in A : \; \Big ( (a,b) \in R \quad \land \quad (b,a) \in R \Big ) \quad \longrightarrow \quad a = b$

Dicho de otra manera, no existen los elementos a, b distintos, y que a este relacionado con b y b este relacionado con a

$\nexists a, b \in A : \; (a,b) \in R \quad \land \quad (b,a) \in R \quad \land \quad a \ne b$

Propiedad transitiva

Artículo principal: Relación transitiva.

Una relación binaria tiene la propiedad transitiva cuando, dado los elementos a, b, c del conjunto, si a esta relacionado con b y b esta relacionado con c, entonces a esta relacionado con c:

$\forall a, b, c \in A : \; \Big ( (a,b) \in R \quad \land \quad (b,c) \in R \Big ) \quad \longrightarrow \quad (a,c) \in R$

miércoles, 20 de junio de 2012

clasificación por tipos de relaciones.

Tomando las rectas en el plano:

Propiedad transitiva